Cenni alla Teoria del Caos e Teoria dei Mercati Frattali
In questo articolo: Teoria dei Mercati Finanziari Caotici Frattali introdotta con la teoria del caos
INDICE CORSO DI BORSA TRADING WAYS
La pubblicità ci consente di portare avanti il sito senza metterci del nostro e mantenendo quella totale autonomia ed indipendenza che ci ha sempre contraddistinto ...
Obiettivo di questa sezione è solo quello di introdurre la teoria del caos ed offire dei cenni in merito alla sua applicazione ai mercati finanziari.
Per comprendere questa teoria si richiede una buona conoscenza matematica, non comune da trovare anche in persone che abbiano una Laurea in Matematica. Cercare di applicare i modelli del caos ai mercati finanaziari (o addirittura realizzare/migliorare questi modelli) richiede invece una forte competenza matematica ed un grande passione per i mercati per poter intepretare e valorizzare i risultati della teoria stessa. Per coloro che non si sono mai cimentati con la disciplina matematica per la spiegazione dei fenomeni naturali od artificiali, devo far presente che il contributo della matematica nella pratica, pur essendo indispensabile, è sovente molto sterile, nel senso che per dimostrare un tesi anche obiettivamente scontata lo sforzo matematico è talvolta incredibilmente elevato; per questo i contributi maggiori nell'ambito della modellistica sono venuti da "fisici ed ingegneri", certamente supportati da spaventose ricerche teoriche di matematici, ma di di cui essi ne hanno colto i concetti senza pretendere di applicare quel metodo di dimostrazione così rigoroso come viene richiesto nella disciplina matematica.
Al tempo stesso, da ricerche condotte su Internet (2005 n.d.r), ho notato che alcune organizzazioni finanaziarie sono oggi fortemente impegnate a studiare ed applicare questi modelli matematici con il supporto di prestigiose Univeristà e centri di ricerca. Il tenativo è quello di modellare il comportamento del mercato con strumenti scientifici e modelli matematici molto complessi ed evoluti, capaci di indirizzare i fallimenti e le carenze delle teorie precedenti. Proprio per questo, a mio avviso, tali ricerche non vengono pubblicizzate proprio per la loro valenza scientifica che evidentemente equivale ad una valenza economica per gli aspetti di capacità predittiva dell'evoluzione dei mercati. Al Dicembre del 2012 abbiamo notizia di strumenti informativi che utilizzano modelli di mercatofrattale per la previsione degli andamenti futuri. Non conosciamo tuttavia maggiori dettagli sul merito tecnico della cosa, in quanto ci siamo concentrati nel corsi degli anni su modellistiche alternative.
Comprendere la Teoria del Caos
Alcuni secoli fà un grande matematico formulò l'ipotesi che conoscendo nel dettaglio le condizioni inziali di un qualsiasi sistema si sarebbe potuto conoscere in anticipo il suo comportamento con un certi margini di precisione, in funzione dell'errore nelle misure iniziali. Si tratta di Pierre Simon Laplace, una scienziato che diede il più grande contributo nello sviluppo della teoria deterministica dell'universo, sviluppata nel periodo 1700-1900. Gran parte delle scoperte per i sistemi della meccanica classica sono dovute proprio a Laplace.
Proprio agli inizi del 1900, Henri Poincaré nel tentativo di spiegare i movimenti dei corpi celesti affermò, in poche parole, che predire il comportamento di alcuni sistemi è impossibile giacchè piccoli cambiamenti nella misura delle condizioni iniziali determinavano gigantesche differenze nella evoluzione dei sistema, e che pertanto piccoli errori di misura nelle condizioni iniziali non producevano piccoli errori nella determinazione delle grandezze finali, contraddicendo uno dei risultati della teoria di Laplace.
I sistemi dinamici, ossia sistemi in cui una grandezza X è funzione del tempo t, sono l'esempio migliore per comprendere cosa sia un sistema caotico e come piccoli cambiamenti alle condizioni iniziali impattino in modo determinante sulle previsioni di evoluzione del sistema. Supponiamo che un sistema sia descritto dalla grandezza X e che conoscendo il valore di X al tempo t, X(t), sia possibile dedurre il valore al tempo t+1 grazie all'uso di una formula iterativa.
La dipendenza da X(t) può essere lineare, ossia X(t+1) può essere descritto da un formula tipo:
X(t+1) = AX(t)+B
dove A e B rappresentano delle costanti o delle variabili che non dipendono da X(t). Un banale sistema dinamico lineare può essere l'altezza di una persona.
Se invece X(t+1) è funzione di una qualche potenza di X(t) si parla di sistema non lineare, che è il sistema che ci interessa in questa trattazione. Un sistema non lineare può essere rappresentato, ad esempio, dalla seguente equazione, detta "equazione logistica:
X(t+1) = A X(t) - B*X(t)*X(t).
In questo caso il motivo di usare il quadrato di X(t) per prevedere X(t+1) è quello di modificare il comportamento lineare con una correzione non fissa, ma funzione degli stessi valori della variabile X(t). Si pensi al prezzo del greggio, al prezzo dell'oro o di un qualsiasi bene. Sarebbe errato descriverlo con l'equazione lineare giacchè il prezzo sarebbe soggetto ad una crescita infinita per valori di A maggiori di 1, mentre sarebbe "attratto" al valore B se A fosse minore di 1 (non a caso per A<1 la formula viene chiamata attrattore lineare). Invece la correzione quadratica è uno dei modi per ragirare questo comportamento ed introdurre una componente di "feedback" del valore (prezzo) X(t)
Come esempio di sistema non lineare, facciamo riferimento all'equazione "logistica" con i coefficienti A e B identici.
X(t+1) = A X(t) - A*X(t)*X(t).
E' chiaramente non lineare per la presenza del quadrato di X, ma la sua caratteristica più peculiare è la forte sensibilità ai valori inziali. Nella figura qui di seguito osserviamo il comportamento della serie X(t) al variare di A, tenendo fisso X(0) a 0,7
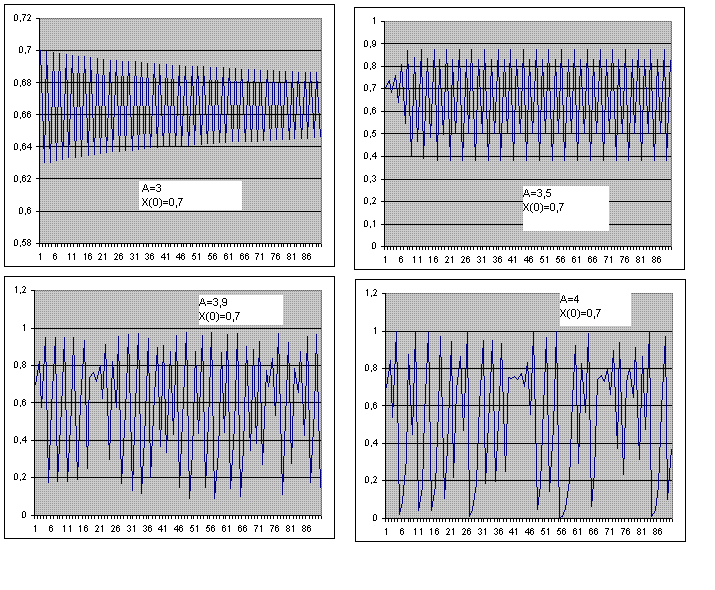
Oltre la sopresa di trovare un comportamento oscillatorio, si noti come la forma cambi da una forma sinusuoidale ad una molto confusa al tendere di A a 4.
Ma le maggiori soprese si osservano tenendo fisso A al valore 4 e cambiando leggermente le condizioni inziali. Al tendere di X(0) a 0.75 la curva diviene caotica nel senso che X(t) assume valori notevolmente differenti (per esempio basti confrontare i valori X(90)); inoltre per X(0) = 0.75 abbiamo un comportamento notevolmente diverso, ossia X(t) si schiaccia sul valore 0.75. Questo comportamento è descritto con il nome di "attrattore strano" (strange attarctor).
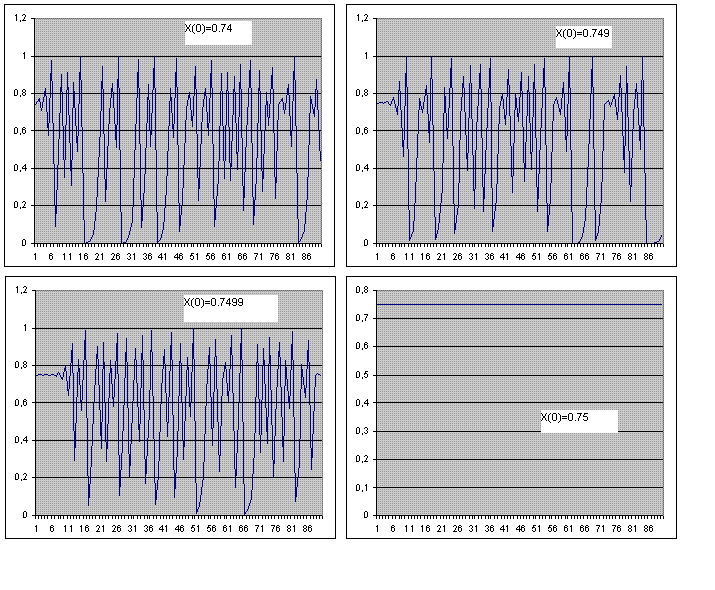
Possiamo dire che l'equazione logistica è un sistema complesso caotico, anche se il caos è solo apparente giacchè la curva è regolata da una equazione ben precisa e molto semplice.
Quello che va ricordato è che quest'ultime figure mostrano un comportamento indubbiamente molto sensibile ai valori iniziali, dopo un certo numero di iterazioni (es dopo 20). Questa figura ha ulteriori caratteristiche quali la ripetitività di certi pattern, su scale differenti, cosa a cui ci si riferisce con il termine "frattale".
Rimando alla tesi laurea di Giancarlo Fabbro come punto di partenza degli studi che sto compiendo alla data del marzo 2005. La tesi, a mio avviso ottima, è disponibile sul sito tesionline con id 5435
E' molto significativo il risultato di Fabbro di aver stimato un esponente di Hurst maggiore di 1/2, cosa che "implica un moto Browniano frazionario (Fractional Brownian Motion o Biased Random Walk), ossia un processo la cui evoluzione è dipendente in qualche misura dagli eventi passati e seguono un andamento nel tempo che può essere descritto come un processo stocastico distorto noto anche come moto Browniano frazionario -FBM-