Introduzione alla Modellista dei Mercati Finanziari

Con la nascita della borsa si sono ricercate, sviluppate e consolidate una serie di teorie specifiche dei mercati finanziari, sia di tipo scientifico/statistico sia di tipo non convenzionale come le teorie di Down, Elliott e Gann.

A partire dal 1950 si è sviluppata la teoria dell'analisi tecnica, oggi molto popolare, che afferisce, a mio avviso, a teorie di mercato non efficiente.Prevede infatti l'uso di strumenti elementari derivati dalla matematica e dalla statistica, quali oscillatori/indicatori, che sono costruiti a partire dalle serie storiche dei titoli e su questi dati analizza e predice, entro certi limiti, l'evoluzione del prodottofinanziario. Fra questi si ricordano i famosi RSI, MACD, ROC ma anche i meno noti Williams %R, TRIX, le Bande di Bollinger, le Parabolic SAR ecc... L'analisi tecnica prevede anche specifiche metodologie d'uso essenzialmente basate sull'uso combinato di quattro tipologie di indicatori (money flow, momento, trend e volatilità) e sullo studio delle forme grafiche delle curve dei prezzi in funzione del tempo (analisi grafica). Questi metodi analitici/previsionali mostrano inefficienze e fallimenti anche laddove si applichi una metodologia d'uso articolata e che vuole assimigliare ad un vero e proprio sistema intelligente di trading.

Già dagli inzi del '900 sono state eseguite ricerche finalizzate a definire dei modelli specifici per i mercati finanziari, applicando modellistiche derivate dalla statistica, dalla fisica e dalla matematica. Da un punto di vista storico le tappe e le toerie fondamentali possono essere riassunte come segue:

• 1964: Modello Random Walk
• 1976: Teoria dei Mercati Efficienti (Efficient Market Hypotesys - EMH)
• 1990: Teoria dei Mercati Coerenti (Coherent Market Hypotesys - CMH)
• 1994: Teoria dei Mercati Frattali (Fractal Market Hypotesys - FMH)

Modello Random Walk e Teoria EMH

A partire dai primi del '900 nella "Theory of Speculation", Louis Bachelier investigò su una modellizzazione dei prezzi dei titoli azionari secondo un modello definito "Random Walk". Questa modellistica si basa sulla ipotesi statistica che i prezzi delle azioni seguano un processo di moto browniano, ovvero random walk, ossia i prezzi sono variabili random indipendenti, identicamente distribuite, normalmente distribuite. Essenzialmente il movimento dipendedalle news sul mercato (principio di efficienza) con un processo di adattamento delle quotazioni più o meno "regolare"

Questa ipotesi fu ripresa nel 1964 da Osborne ed anche da Paul Cootner in un'opera dal titolo "The random character of stock market prices", facendo uso di strumenti matematici/statistici derivati dalla scoperta di Einstein dell'equazione che regola il fenomeno del moto random delle molecole, noto come moto Browniano. Esistono diversi modelli di random walk, fra cui il Martingale che non assume la restrizione della identica distribuzione delle variabili, ma la logica comune che sovraintende questo tipo di modellistica è quella del mercato efficiente (EMH), formalizzata da Fama nel 1976, ovvero sull'assunzione che i prezzi riflettono immediatamente e pienamente tutte le informazioni disponibili sul mercato.

Questo modello implica che l'evoluzione del prezzo di uno strumento finanziario è essenzialmente casuale e la migliore previsione del prezzo dell'istante successivo non può che essere fatta sulla base del prezzo precedente e delle informazioni disponibili al mercato (investitori). Pertanto i movimenti dei prezzi e dei rendimenti non seguono alcun trend o regolarità e quindi i movimenti passati non possono essere usati per previsioni future. Il mercato è completamente efficiente nel processare le informazioni disponibili e dunque ad aggiustare i prezzi completamente ed instantaneamente.

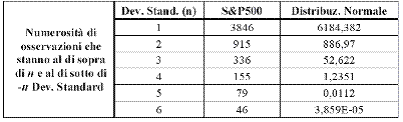
La verifica sperimentale della teoria ha evidenziato contraddizioni nell'analisi dei rendimenti che contraddicono l'ipotesi del modello "Random Walk". Nelle serie storiche reali (di indici, rendimenti azionari, tassi di interesse ecc..) le distribuzioni dei rendimenti si presentano in forme diverse da quella Gaussiana. A titolo di esempio si riporta nella seguente tabella la numerosità delle variazioni percentuali ad un giorno dello Standard & Poor's 500 che cadono nelle code della distribuzione per diverse ampiezze delle stesse. Si noti come a partire da devizione standard uguale a 3 le code della distribuzione del campione sono sempre più spesse di quelle di una normale, dimostrando quindi un cattivo adattamento della distribuzione normale alla descrizione del fenomeno.

Fama propose 3 diversi modelli di mercato efficiente: la forma debole, la forma semi-forte e la forma forte. Con tali forme si cerca essenzialmente di spiegare tali incogruenze attraverso la modalità con cui il mercato processi le informazioni disponibili, ovvero come il flusso di informazioni pubbliche e private impatti sulla dinamica dei prezzi secondo meccanismi graduali di efficienza. In contrapposizione al modello EMH emersero le teorie dei mercati inefficienti (Inefficient Market Hypothesis - IMH) e quella del mercato Frattale (FMH)

Modello di Mercato Frattale (FMH) e sistemi Caotici

Nel 1963 Mandelbrot, per spiegare il fenomeno della leptocurtosi riscontrato nelle distribuzioni dei rendimenti, propose al posto della distribuzione normale una famiglia di distribuzioni chiamate Pareto/Levy stabili, ovvero distribuzioni stabili cioè invarianti in somma. Senza entrare nei dettagli matematici, peraltro molto complessi, questa modellistica implica caratteristiche di:

• invarianza in somma (la somma di due o più distribuzioni frattali con stesso esponente caratteristico mantiene la stessa forma)
• self-similarity (autosomiglianza in scala)
• discontinuità (effetto Noah di Mandelbrot ovvero variazioni sensibili, improvvise e discontinue quando i mercati perdono la loro struttura frattale).

Gli studi di Mandelbrot e successivamente di Peters aprono all'applicazione di nuove modellistiche derivate dai sistemi dinamici non lineari o sistemi caotici. Tali sistemi sono regolati da una legge deterministica molto complessa, comprendente una componente di feedback, ed inoltre sono particolarmente sensibili alle condizioni iniziali, ovvero piccole differenze nella condizione iniziale determinano delle differenze molto grosse nel fenomeno finale. Inoltre i sistemi caotici presentano comportamenti che alternano combinazioni di ordine e disordine, con delle transizioni discontinue, e presentano dei cicli non periodici e di trend-reinforcing. Tutto ciò è ragionevolmente vicino al comportamento dei mercati e degli strumenti finanziari.

Nel 1991 Edgard Peters affermò che l'andamento delle serie storiche dei rendimenti su base giornaliera, settimanale e mensile (dell'indice S&P 500) per 40 osservazioni successive risultano assolutamente simili e non distinguibili nel caso in cui non vengano specificate le scale sugli assi, dunque riconoscendo una auto-somiglianza qualitativa, in senso temporale, delle serie storiche ed aprendo dunque alla Fractal Market Hypothesis.

La teoria FMH, che cerca di spiegare i risultati sperimentali riscontrati, si basa su due concetti chiave: la liquidità dei mercati finanziari e la stabilità. La liquidità, che non è assolutamente presa in considerazione nella EMH, permette da un lato di giustificare la stabilità del mercato (giacchè gli investitori di lungo termine sono disposti ad acquistare strumenti finanziari non ritenuti desiderabili da quelli breve termine) e dall'altro spiega i meccanismi di crash del sistema laddove manchi la richiesta, dunque venga meno la liquidità (denaro su book), rompendone la struttura frattale.

Nell'ambito della teoria fisico-matematica dei sistemi caotici/frattali riverste particolare importanza la Rescaled Range Analysis (Analisi R/S) e l'Esponente di Hurst (H) giacchè:

• per 0<H<½ la serie storica è antipersistente, quindi tende ad invertire il trend
• per H=½ si ricade in un moto browniano o random walk
• per ½<H<1 la serie storica è persistente, dunque è caratterizzata da un comportamento di memoria, forte dipendenza dalle condizioni iniziali, assenza di una scala temporale caratterizzante dunque comportamento di autosomiglianza.

E' molto significativo il risultato di alcuni ricercatori di aver stimato un esponente di Hurst maggiore di ½ per gran parte delle serie storiche dei prezzi dei titoli, cosa che implica un moto Browniano frazionario (Fractional Brownian Motion o Biased Random Walk) ossia un processo la cui evoluzione è dipendente in qualche misura dagli eventi passati con un tipo effetto di memoria teso alla stabilità del processo. Volendo dare un esempio si cita una esperienza recente in cui si sono confrontati i vari risultati di Peters con quelli attuali. In particolare Peters ha elaborato serie storiche del periodo 1963 - 1989, mentre questi risultati sono di serie storiche di prezzi del periodo 1970 - 2000. Il titolo scelto, a titolo di esempio, è quello della Coca Cola (NASDAQ: KO) per il quale Peters stimò H = 0,70 e un ciclo di 42 mesi. Le recenti indagi rilevano invece due cicli, rispettivamente di 27 e 50 mesi con H = 0,649 per il primo e H = 0,807 per il secondo. Nella figura seguente è riportato il grafico dell'analisi R/S per questo titolo. Si osservano due cambi strutturali, il primo a log(n) = 1,43 e il secondo a log(n) = 1,70 (le rette di regressione si adattano alla pendenza media dei due segmenti). Inoltre per testare la correttezza dell'individuazione dei due punti si è ricorso al test di cambio strutturale Chow.

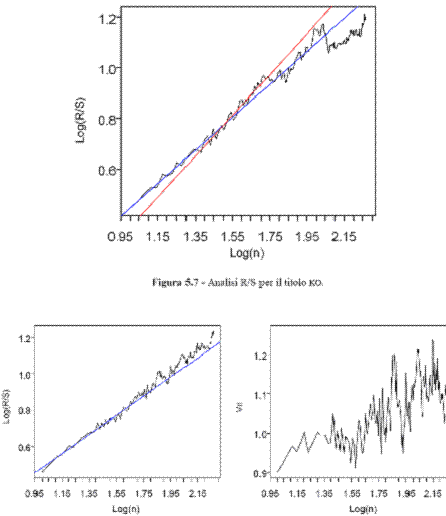
In conclusione con l'analisi R/S, l'assunzione d'indipendenza di lungo periodo è smentita. La serie dei rendimenti è una serie persistente con una sottostante distribuzione di probabilità frattale. I titolo segue un processo stocastico distorto (biased) esibendo un comportamento trend-reinforcing.

Teoria dei Mercati Coerenti (CMH)

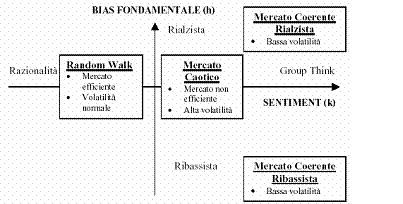
Nel 1990 Vaga avanzò una nuova teoria dei mercati, ovvero quella del mercato Coerente (CMH), basata su 4 fasi principali: random, transizione, caotica e corente.

Tale teoria si basa su dei parametri fondamentali quali il rendimento dei titoli azionari, il sentiment degli investitori, il bias (polarizzazione/attrazione) dei fondamentali.

Questo modello prevede che il mercato transiti in 3 fasi principali: la fase di Random Walk (caratterizzata da poca volatilità ed alta efficienza), la fase di mercato caotico (caratterizzato da scarsa efficienza ed elevata volatilità) ed infine mercato coerente rialzista/ribassista derivato dal consolidarsi del sentiment degli investitori.